Unit 1.2.1: Long Division Method
A polynomial in one variable is any expression of the type \[ a_nx^n + a_{n-1} x^{n-1} + … + a_2x^2 + a_1x+a_0, \]
where \( n \) is non-negative integer and \( a_n, a_{n-1} … a_0 \) are real numbers, called coefficients. \(a_nx^n \) is called the leading term of the polynomial. \( 'n' \) is degree of the polynomial.
(b) If \( p(x), q(x), d(x) \) and \( r(x) \) represent polynomial, quotient, divisor and remainder respectively. Write the relation among them. Solution: We know, Polynomial = Divisor x Quotient + Remainder
Quotient \( Q(x) = x - 7 \) and remainder \( ( R ) = 0 \)
(b) \( x^3 + 2x^2 -5x-6 \div (x+1) \)
Solution:
Quotient \( Q(x) = x^2 + 2x + 4 \) and Remainder \( R = 0 \)
(d) \( x^3+9x^2+27x+27 \div (x+3) \)
Solution:
Quotient \( Q(x) = x^2 + 6x +9 \) and Remainder \( (R) = 0 \)
3. Divide using long division method and find quotient and remainder.
(a) \( x^3 + 2x^2 -5x -7 \div (x+1) \)
Solution:
Quotient \( Q(x) = x^2 + x -6 \) and Remainder \( R = - 1 \)
(b) \( x^3 - 10x^2 + 16x + 26 \div (x-5) \)Solution:
Quotient \( Q(x) = x^2 - 5x - 9 \) and Remainder \( R = -19 \)
(c) \( 2x^4+5x^2-3x-7 \div ( 2x-1 ) \)
Solution:
Quotient \( Q(x) = x^3 + \frac{1}{2} x^2 + \frac{11}{4} x - \frac{1}{8} \) and Remainder \( (R) = \frac{-57}{8} \)
(d) \( y^5 +y^3 - y \div (3-y) \)
Solution:
Quotient \( Q(y) = -y^4 - 3y^3 - 10y^2 - 30y - 89 \) and Remainder \( (R) = 267 \)
4. For the function \( f(y) = y^3 – y^2 – 17y – 15,\) use long division to determine whether each of the following is a factor of \( f(y) \) or not.
(a) \( y + 1 \)
Solution:
Here, remainder is 0. So \( y + 1 \) is a factor of \( f(y) \).
(b) \( y + 3 \)
Solution:
Since, remainder is 0, \( y + 3 \) is a factor of \( f(y) \).
(c) \( y + 5 \)
Solution:
As remainder \( = - 80 \neq 0 \), \( y + 5 \) is not factor of \( f(y) \)
(d) \( y - 1 \)
Solution:
As remainder \( = -30 \neq 0 \),\( y - 1 \) is not a factor of \( f(y) \).
(e) \( y -5 \)
Solution:
As remainder \( = 0, y - 5 \) is a factor of \( f(y) \)
5. For the polynomial \( p(x) = x^4 – 6x^3 + x – 2 \) and divisor \( d(x) = x – 1, \) use long division to find the quotient \( Q(x) \) and the remainder \( R(x) \) when \( P(x) \) is divided by \( d(x).\) Express \( p(x) \) in the form of \( d(x). Q(x) + R(x). \) Write your finding.
Solution:
Here, \begin{align} p(x) & = x^4 - 6x^3 +x - 2 \\ d(x) & = x - 1 \end{align}
Now,
Hence, Quotient \( Q(x) = x^3 - 5x^2 - 5x - 4 \)
Remainder \( (R) = - 6 \)
We know, \( p(x) = d(x). Q(x) + R(x) \)
\( x^4 - 6x^3 + x - 2 = (x-1)(x^3-5x^2-5x-4) - 6 \)
Unit: 1.2.2 : Synthetic Division
1. (a) What is the degree of quotient when the degree of polynomial is 'n' in synthetic division?
Solution: The degree of quotient is \( n - 1 \). 1. (b) What should be the expression of division in synthetic division? Solution: In synthetic division the divisor must be linear and dividend must be in standard form. 2. Use synthetic division and divide in each of the following: (a) \( x^3 +8 \) by \( x - 2 \) Solution: Let \( f(x) = x^3 + 8 \) Zero of \( x - 2 \) is 2. Using synthetic division, we get,
Here, quotient \( = 2x^3 + x^2 - 3x + 10 \)
Remainder \( = -42 \)
2. (c) \( 4x^3 - 3x^2 + x + 9 \) by \( x -2 \)
Solution:
Let, \( f(x) = 4x^3 - 3x^2 + x + 9 \)
Zero of polynomial \( x - 2 \) is 2.
Now, using synthetic division, we get,
Quotient \( = 4x^2 + 5x + 11 \)
Remainder \( = 31 \)
2. (d) \( 2x^3 + 7x^2 - 8 \) by \( ( x + 3 ) \)
Solution:
Let, \( f(x) = 2x^3 + 7x^2 + 0.x - 8 \) 
Here, Quotient \( = 2x^2 + x - 3 \)
Remainder \( = 1 \)
2. (e) \( 8x^3 + 4x^2 + 6x - 7 \) by \( 2x - 1 \)
Solution:
Let, \( f(x) = 8x^3 + 4x^2 + 6x - 7 \)
Here,♠♠♠All The Best ♠♠♠
Unit 1.2.3(A): Remainder Theorem
1. (a) State remainder theorem.
Solution:
If a polynomial \( f(x) \) is divided by \( x-a \) then the remainder is \( f(a) \).
1. (b) If \( ax + b ( a \neq 0 ) \) divides \( f(x), \) what is the remainder ?
Solution:
Here, zero of polynomial \( ax+b \text{ is } \frac{-b}{a} \).
Remainder \( = f\left(\frac{-b}{a} \right) \)
2. Use remainder theorem and find the remainder in each of the following:
(a) \( (2x^3-5x^2+x-5 ) \div (x-2) \)
Solution:
Let, \( f(x) = 2x^3-5x^2+x-5 \)
Zero of polynomial \( x-2 \) is 2.
\begin{align} \text{Remainder } & = f(2) \\ & = 2(2)^3-5(2)^2+2-5 \\ & = 2 \times 8 -5 \times 4 +2 -5 \\ & = 16-20+2-5 \\ & = - 7 \end{align}
(b) \( (4x^3+7x^2-3x+2)\div (x+2) \)
Solution:
Let, \( f(x) = 4x^3+7x^2-3x+2 \)
Zero of polynomial \( x+2 \) is \( -2 \)
\begin{align} \text{Remainder } & = f(-2) \\ & = 4(-2)^3+7(-2)^2-3(-2)+2 \\ & = 4 (-8) +7(4)+6+2 \\ & = -32+28+6+2 \\ & = 4 \end{align}
(c) \( (x^4-3x^2+15) \div (x-1) \)
Solution:
Let, \( f(x) =x^4-3x^2+15 \)
Zero of polynomial \( x-1 \) is \( 1 \)
\begin{align} \text{Remainder } & = f(1) \\ & = 1^4-3(1)^2+15 \\ & =1-3+15\\ & = 13 \end{align}
(d) \( (x^5+x^3+20) \div (2x-1) \)
Solution:
Solution:
Let, \( f(x) =x^5+x^3+20 \)
Zero of polynomial \( 2x-1 \) is \( \frac{1}{2} \)
\begin{align} \text{Remainder } & = f\left(\frac{1}{2}\right) \\ & = \left(\frac{1}{2} \right)^5+\left( \frac{1}{2} \right)^3 +20\\ & =\frac{1}{32}+\frac{1}{8} + 20 \\ & = \frac{1+4+ 32\times 20}{32} \\ & = \frac{1+4+640}{32} \\ & =\frac{645}{32} \end{align}
(e) \( 7x^4-6x^3+8x^2-10x+9 \div (3x-9) \)
Solution:
Let, \( f(x) =7x^4-6x^3+8x^2-10x+9 \)
Zero of polynomial \( 3x-9 \) is \( 3 \)
\begin{align} \text{Remainder } & = f(3) \\ & = 7(3)^4-6(3)^3+8(3)^2-10(3)+9 \\ & = 7(81)-6( 27)+8(9) -30+9 \\ & = 567-162+72-30+9 \\ & = 456 \end{align}
(f) \( 6x^4-4x^3+6x^2+8x+10 \div (2x+3) \)
Solution:
Let, \( f(x) =6x^4-4x^3+6x^2+8x+10 \)
Zero of polynomial \( 2x+3 \) is \( \frac{-3}{2} \)
\begin{align} \text{Remainder } & = f\left( \frac{-3}{2}\right) \\ & = 6\left(\frac{-3}{2} \right)^4 - 4 \left( \frac{-3}{2} \right)^3 +6 \left( \frac{-3}{2} \right)^2 +8\left( \frac{-3}{2} \right) + 10 \\ & = 6 \left( \frac{ 81}{16} \right) -4 \left(\frac{-27 }{8} \right) + 6\left( \frac{9}{4} \right) - 12 + 10 \\ & = \\ & = 3\times \frac{81}{8} + \frac{27}{2}+ 3\times \frac{9}{2} - 2 \\ & = \frac{3\times 81+4\times 27 + 4\times 27 - 2\times 8}{32} \\ & = \frac{243+108+108-16 }{ 8 } \\ & =\frac{443}{8 } \end{align}
(g) \( 9x^5-7x^2+12x+10 \div (3x+1) \)
Solution:
Let, \( f(x) = 9x^5-7x^2+12x+10 \)
Zero of polynomial \( 3x+1 \) is \( \frac{-1}{3} \)
\begin{align} \text{Remainder } & = f\left( \frac{-1}{3} \right) \\ & = 9\left(\frac{-1}{3} \right)^5 - 7 \left( \frac{-1}{3} \right)^2 +12 \left( \frac{-1}{3} \right) + 10 \\ & = 9 \left( \frac{ -1}{243} \right) - 7 \left(\frac{1 }{ 9} \right) -4 + 10 \\ & = \\ & = \frac{-1}{27}-\frac{7}{9}+6 \\ & = \frac{-1-7\times 3 + 27 \times 6 }{27} \\ & = \frac{-1-21+162 }{ 27 } \\ & =\frac{140}{27} \end{align}
3. (a) If \( x^4+2x^2-4x+k \) is divided by \( x-2 \), the remainder is 4, find the value of \( k \), using remainder theorem.
Solution:
Let, \( f(x) = x^4+2x^2-4x+k \)
Zero of \( x-2 \) is 2.
\begin{align} & \text{Remainder } = 4 \\ & \text{ or, } f(2) = 4 \\ & \text{ or, } (2)^4+2(2)^2-4(2)+k = 4\\ & \text{ or, } 16+8-8+k = 4 \\ & \text{ or, } 16 + k = 4 \\ & \text{ or, } k = 4 - 16 \\ & \therefore k = - 12 \end{align}
3. (b) If \( x^3-9x^2+(k+1)x-8 \) is divided by \( x-5 \), the remainder is 6, find the value of \( k \), using remainder theorem.
Solution:
Let, \( f(x) = x^3-9x^2+(k+1)x-8 \)
Zero of \( x-5 \) is 5.
\begin{align} & \text{Remainder } = 6 \\ & \text{ or, } f(5 ) = 6 \\ & \text{ or, } 5^3 - 9 (5)^2 +(k+1) (5) - 8 = 6 \\ & \text{ or, } 125 - 225 +5k + 5 - 8 = 6 \\ & \text{ or, } 5k - 97 = 6 \\ & \text{ or, } 5k = 6+97 \\ & \text{ or, } 5k = 103 \\ & \therefore k = \frac{103}{5} \end{align}
3. (c) If \( x^3-ax^2+8x+11 \) and \( 3x^3-ax^2+7ax+13 \), both are divided by \( (x-1) \), remainder is same, find the value of \( a \).
Solution:
Let, \( f(x) = x^3-ax^2+8x+11 \)
And \( g(x) = 3x^3-ax^2+7ax+13 \)
Zero of \( x-1 \) is 1.
By question the remainder is same,
so,
\begin{align} & f(1) = g(1) \\ & \text{or, } 1^3 - a(1)^2+8(1)+11 = 3(1)^3-a(1)^2+7a(1)+13 \\ & \text{or, } 1 - a + 8 + 11 = 3 - a + 7a +13 \\ & \text{or, } 20 = 7a +16 \\ & \text{or, } 20-16 = 7a \\ & \text{or, } 4 = 7a \\ & \text{or, } 7a = 4 \\ & \therefore a = \frac{4}{7} \end{align}
3. (d) If \( (x-2) \) divides the polynomials \( 4x^3+2x^2+kx+5 \) and \( kx^2+5x+4 \) to get the same remainder, find the value of \( k \).
Solution:
Let, \( f(x) = 4x^3+2x^2+kx+5 \)
And \( g(x) = kx^2+5x+4 \)
Zero of \( x-2 \) is 2.
By question the remainder is same,
so,
\begin{align} & f(2) = g(2) \\ & \text{or, } 4(2)^3+2(2)^2+k(2)+5 = k(2)^2+5(2)+4 \\ & \text{or, } 4(8)+2(4)+2k+5=k(4)+10+4 \\ & \text{or, } 32+8+2k+5 = 4k + 14 \\ & \text{or, } 45-14 = 4k-2k \\ & \text{or, } 31 = 2k \\ & \text{or, } 2k = 31 \\ & \therefore k = \frac{31}{2} \end{align}
♠♠♠All The Best ♠♠♠
Unit 1.2.3 (B) : Factor Theorem
Solution:
If \( x-a \) is a factor of \( f(x) \) then \( f(a) = 0 \)
OR
If \( f(a) = 0 \) then \( x-a \) is a factor of \( f(x) \).
1. (b) If \( (x-a) \) is a factor of \( x^n - a^n \), what is the degree of quotient.
Solution:
The degree of quotient is \( n - 1 \).
2. In each of the following, use factor theorem to find whether \( g(x) \) is a factor of polynomial \( f(x) \) or not?
(a) \( f(x) = x^3 + 9x^2 + 27x + 27; \ \ \ g(x) = x + 3 \)
Solution:
Here, \( f(x) = x^3+9x^2+27x+27 \)
And \( g(x) = x+ 3 \)
Zero of \( x+3 \) is \( - 3 \)
\begin{align} \text{ Remainder } & = f (-3) \\ & = (-3)^3+9(-3)^2+27(-3) + 27 \\ & = -27 + 81 - 81 + 27 \\ & = 0 \end{align}
\( \therefore \ g(x) \) is a factor of polynomial \( f(x).\)
(b)\( f(x) = x^3 + x^2 + 27x + 27, g(x) = x + 3 \)
Solution:
Here, \( f(x) = x^3+x^2+27x+27 \)
And \( g(x) = x+3 \)
Zero of \( x+3 \).
\begin{align} \text{Remainder } & = f(-3) \\ & = (-3)^3+(-3)^2+27(-3)+27\\ & = -27 +9 - 81 +27 \\ & = -72 \neq 0 \end{align}
\( \therefore g(x) \) is not a factor of polynomial \( f(x) \).
(c) \( f(x) = x^3 + 6x^2 + 7x + 9, g(x) = x – 2 \)
Solution:
Here, \( f(x) = x^3+6x^2+7x+9 \)
And \( g(x) = x-2 \)
Zero of \( x-2 \) is 2.
\begin{align} \text{Remainder } & = f(2) \\ & = 2^3+6(2)^2+7(2)+9 \\ & = 8 + 24 + 14 + 9 \\ & = 55 \neq 0 \end{align}
\( \therefore g(x) \) is not a factor of polynomial \( f(x) \).
(d) \( f(x) = 3x^3 + x^2 – 20x + 12, g(x) = 3x – 2 \)
Solution:
Here, \( f(x) = 3x^3 + x^2 – 20x + 12 \)
And \( g(x) = 3x – 2 \)
Zero of \( 3x – 2 \) is \( \frac{2}{3} \).
\begin{align} \text{Remainder } & = f\left(\frac{2}{3}\right) \\ & = 3\left(\frac{2}{3}\right) ^3+\left(\frac{2}{3}\right) ^2-20\left(\frac{2}{3}\right) +12 \\ & = 3\left(\frac{8}{27}\right) + \frac{4}{9}-\frac{40}{3} +12 \\ & = \frac{8+4-40\times 3 + 12\times 9 }{9} \\ & = \frac{8+4-120+180}{9} \\ & = \frac{0}{9} \\ & = 0 \end{align}
\( \therefore g(x) \) is a factor of polynomial \( f(x) \).
(e) \( f(x) = 8x^3 – 4x^2 + 7x + 9; g(x) = 2x + 1 \)
Solution:
Here, \( f(x) = 8x^3 – 4x^2 + 7x + 9 \)
And \( g(x) = 2x + 1 \)
Zero of \( 2x + 1 \) is \( \frac{-1}{2} \).
\begin{align} \text{Remainder } & = f\left(\frac{-1}{2}\right) \\ & = 8\left(\frac{-1}{2}\right)^3-4\left(\frac{-1}{2}\right)^2+7\left(\frac{-1}{2}\right)+9 \\ & = 8\left(\frac{-1}{8}\right) -4\left(\frac{1}{4}\right)-\frac{7}{2}+9 \\ & = -1-1-\frac{7}{2}+9 \\ & = \frac{-2-2-7+18}{2} \\ & = \frac{7}{2} \neq 0 \end{align}
\( \therefore g(x) \) is not a factor of polynomial \( f(x) \).
3. (a) Find the value of \( k \) , if \( x + 3 \) is a factor of \( 3x^2 + kx + 6 \)
Solution:
Let, \( f(x) = 3x^2+kx+6 \)
Zero of \( x+3 \) is -3.
As \( x+3 \) is a factor of f(x),
\begin{align} & \text{Remainder } = 0 \\ & \text{ or, } f(-3 ) = 0 \\ & \text{ or, } 3(-3)^2+k(-3)+6=0 \\ & \text{ or, } 27-3k+6=0 \\ & \text{ or, } 33=3k \\ & \text{ or, } k=\frac{33}{11} \\ & \therefore k=11 \end{align}
3. (b) Find the value of \( k \), if \( x + 1\) is a factor of \( x^3 – kx^2 – 3x – 6 \)
Solution:
Let, \( f(x) = x^3 – kx^2 – 3x – 6 \)
Zero of \( x+1 \) is -1.
As \( x+3 \) is a factor of f(x),
\begin{align} & \text{Remainder } = 0 \\ & \text{ or, } f(-1 ) = 0 \\ & \text{ or, } (-1)^3-k(-1)^2-3(-1)-6 =0 \\ & \text{ or, } -1-k+3-6=0 \\ & \text{ or, } -k-4=0 \\ & \text{ or, } -k=4 \\ & \therefore k=-4 \end{align}
3. (c) Find the value of \( m \), for which \( 2x^4 – 4x^3 + mx^2 + 2x + 1 \) is exactly divisible by \(1 – 2x.\)
Solution:
Let, \( f(x) = 2x^4 – 4x^3 + mx^2 + 2x + 1 \)
Zero of \( 1 – 2x \) is \( \frac{1}{2} \) .
As \( 1 – 2x \) is a factor of f(x),
\begin{align} & \text{Remainder } = 0 \\ & \text{ or, } f( \frac{1}{2}) = 0 \\ & \text{ or, } 2\left( \frac{1}{2} \right)^4 -4 \left( \frac{1}{2} \right)^3 +m\left( \frac{1}{2} \right)^2 +2\left( \frac{1}{2}\right)+1=0 \\ & \text{ or, } 2\times \frac{1}{16} -4\times \frac{1}{8} +m\times \frac{1}{4}+1+1=0\\ & \text{ or, } \frac{1}{8}-\frac{1}{2}+\frac{m}{4}+2=0 \\ & \text{ or, } \frac{1-4+2m+16}{8} = 0 \\ & \text{ or, } 2m+13 = 0 \\ & \text{ or, } 2m= -13 \\ & \therefore m = - \frac{13}{2} \end{align}
4. Factorize the following by using factor theorem.
(a) \( 2x^3 + 3x^2 – 3x – 2 \)
Solution:
Let, \( f(x) = 2x^3 + 3x^2 – 3x – 2 \)
Possible factors of 2 are \( \pm 1, \pm 2 \)
\begin{align} \text{Now}, \\ f(1) & = 2(1)^3+3(1)^2 -3(1)-2 \\ & = 2 +3-3 -2 \\ & = 0 \end{align}
\( \therefore x-1 \) is a factor of \( f(x) \)
Now, using synthetic division, we get,
\begin{align} \text{Quotient } & = 2x^2+5x+2 \\ & = 2x^2 +(4+1)x +2 \\ & = 2x^2 +4x+x+2 \\ & = 2x(x+2) +1 (x+2) \\ & = (x+2)(2x+1) \\ \therefore f(x) & = (x-1) (x+2) (2x+1) \end{align}
(b) \( x^3 + 2x^2 - x -2 \)
Solution:
Let, \( f(x) = x^3 + 2x^2 - x -2 \)
Possible factors of 2 are \( \pm 1, \pm 2 \)
\begin{align} \text{Now}, \\ f(1) & = (1)^3+2(1)^2 -1-2 \\ & = 1+2-1-2 \\ & = 0 \end{align}
\( \therefore x-1 \) is a factor of \( f(x) \)
Now, using synthetic division, we get,
\begin{align} \text{Quotient } & = x^2+3x+2 \\ & = x^2 +(2+1)x +2 \\ & = x^2 + 2x +x +2 \\ & = x(x+2)+1(x+2) \\ & = (x+2)(x+1) \\ \therefore f(x) & = (x-1)(x+2)(x+1) \end{align}
(c) \( y^3 - 6y^2 + 3y + 10 \)
Solution:
Let, \( f(y) = y^3 - 6y^2 + 3y + 10 \)
Possible factors of 2 are \( \pm 1, \pm 2 , \pm 5, \pm 10 \)
\begin{align} \text{Now}, \\ f(2) & = 2^3-6(2)^2+3(2)+10 \\ & = 8-24+6+10 \\ & = 0 \end{align}
\( \therefore y -2 \) is a factor of \( f(y) \)
Now, using synthetic division, we get,
\begin{align} f(y) & = y^2 - 4y -5 \\ & = y^2 - (5-1)y-5 \\ & = y^2 -5y + y -5 \\ & = y(y-5) +1(y-5) \\ & = (y-5)(y+1) \\ \therefore f(y) & = (y-2)(y-5)(y+1) \end{align}
(d) \( x^3 + 13x^2 + 32x + 20 \)
Solution:
Let, \( f(x) = x^3 + 13x^2 + 32x + 20 \)
Possible factors of 2 are \( \pm 1, \pm 2, \pm 4, \pm 5, \pm 10, \pm 20 \)
\begin{align} \text{Now}, \\ f(-2) & = (-2)^3+13(-2)^2+32(-2)+20 \\ & = -8+52-64+20 \\ & = 0 \end{align}
\( \therefore x+2 \) is a factor of \( f(x) \)
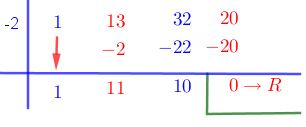
Now, using synthetic division, we get,
\begin{align} \text{Quotient } & = x^2 + 11x+ 10 \\ & = x^2 + 10x + x + 10 \\ & = x(x+10) + 1( x+10) \\ & = (x+10)(x+1) \\ \therefore f(x) & = (x+1)(x+2)(x+10) \end{align}
(e) \( 2x^3 + x^2 – 2x – 1 \)
Solution:
Let, \( f(x) = 2x^3 + x^2 – 2x – 1 \)
Possible factors of 2 are \( \pm 1, \pm \frac{1}{2} \)
\begin{align} \text{Now}, \\ f(1) & = 2(1)^3+1^2-2(1)-2 \\ & = 2+1-2-1 \\ & = 0 \end{align}
\( \therefore x-1 \) is a factor of \( f(x) \)
Now, using synthetic division, we get,
\begin{align} \text{Quotient} & = 2x^2+3x+1 \\ & = 2x^2 + 2x + x + 1 \\ & = 2x(x+1) + 1(x+1) \\ & = (x+1)(2x+1) \\ \therefore f(x) & = (x-1)(x+1)(2x+1) \end{align}
(f) \( x^3 – 23x^2 + 142x – 120 \)
Solution:
Let, \( f(x) = x^3 – 23x^2 + 142x – 120 \)
Possible factors of 2 are \( \pm 1, \pm 2, \pm 3, \pm 5 \text{ etc } \)
\begin{align} \text{Now}, \\ f(1) & = 1^3-23(1)^2+142(1)-120 \\ & =1 -23 + 142 -120 \\ & = 0 \end{align}
\( \therefore x-1 \) is a factor of \( f(x) \)
Now, using synthetic division, we get,
\begin{align} \text{Quotient } & = x^2 - 22x + 120 \\ & = x^2 - 12x - 10x +120 \\ & = x(x-12) -10(x-12) \\ & = (x-12)(x-10) \\ \therefore f(x) & = (x-1)(x-10)(x-12) \end{align}
(g) \( (x – 1) (2x^2 + 15x + 15) – 21 \)
Solution:
\begin{align} \text{Let, } f(x) & = (x – 1) (2x^2 + 15x + 15) – 21\\ & = 2x^3 +15x^2+15x-2x^2-15x-15-2 \\ & = 2x^3+13x^2-36 \end{align}
Possible factors of 36 are \( \pm 1, \pm 2, \pm 3, \pm 4 \text{ etc } \)
\begin{align} \text{Now}, \\ f(-2) & = 2(-2)^3+13(-2)^2-36 \\ & =-16+52-36 \\ & = 0 \end{align}
\( \therefore x+2 \) is a factor of \( f(x) \)
Now, using synthetic division, we get,
\begin{align} \text{Quotient } & = 2x^2+9x-18 \\ & = 2x^2 +12x - 3x - 18 \\ & = 2x(x+6) -3 (x+6) \\ & = (x+6)(2x-3) \\ \therefore f(x) & = (x+2)(x+6)(2x-3) \end{align}
5. Use factor theorem and solve for \( x \).
(a) \( x^3 – 4x^2 – 7x + 10 = 0 \)
Solution:
Let \( f(x) = x^3-4x^2-7x+10 \)
Possible factors of 10 are \( \pm 1, \pm 2, \pm 5, \pm 10 \)
\begin{align} \text{Now, } f(1) & = 1^3-4(1)^2-7(1)+10 \\ & = 1-4-7+10 \\ & = 0 \end{align}
\( \therefore x-1 \) is a factor of \( f(x) \)
Now, using synthetic division, we get,
\begin{align} \text{Quotient } & = x^2 - 3x -10 \\ & = x^2 -5x + 2x - 10 \\ & = x(x-5) + 2(x-5) \\ & = (x-5)(x+2) \\ \therefore f(x) & = (x-1)(x-5)(x+2) \\ \text{or, } 0 & = (x-1)(x-5)(x+2) \end{align}
| Either | OR | OR |
|---|---|---|
| \( x - 1 = 0 \) | \( x - 5 = 0\) | \( x + 2 = 0 \) |
| or, \( x = 1 \) | or, \( x = 5 \) | or, \( x = -2 \) |
\( \therefore x= 1, 5, -2 \)
(b) \( x^3 + 4x^2 + x – 6 = 0 \)
Solution:
Let \( f(x) = x^3+4x^2+x-6 \)
Possible factors of 6 are \( \pm 1, \pm 2, \pm 3, \pm 6 \)
\begin{align} \text{ Now, } f(1) & = 1^3+4(1)^2+1-6 \\ & = 1+4+1 -6 \\ & = 6-6 \\ & = 0 \end{align}
\( \therefore x-1 \) is a factor of \( f(x) \)
Now, using synthetic division,
\begin{align} \text{ Quotient } & = x^2 +5x+6 \\ & = x^2 +3x+2x+6 \\ & = x(x+3) +2 (x+3) \\ & = (x+3)(x+2) \\ \therefore f(x) & = (x-1)(x+2) (x+3) \\ \text{or, } 0 & = (x-1)(x+2)(x+3) \end{align}
| Either | OR | OR |
|---|---|---|
| \( x - 1 = 0 \) | \( x +2 = 0\) | \( x + 3 = 0 \) |
| or, \( x = 1 \) | or, \( x = -2 \) | or, \( x = -3 \) |
\( \therefore x = 1, -2, -3 \)
(c) \( 3x^3 – x^2 – 3x + 1 = 0 \)
Solution:
Let \( f(x) = 3x^3-x^2-3x+1 \)
Possible factors are \( \pm 1, \pm \frac{1}{3} \)
\begin{align} \text{Now, } f(1) &= 3(1)^3-1^2-3(1)+1 \\ & = 3-1-3+1 \\ & = 0 \end{align}
\( \therefore x - 1 \) is a factor of \( f(x) \)
Now, using synthetic division, we get,
\begin{align} \text{Quotient} & = 3x^2 +2x-1 \\ & = 3x^2+3x-x-1 \\ & = 3x(x+1) -1(x+1) \\ & = (x+1)(3x-1)\\ \therefore f(x) & = (x-1)(x+1)(3x-1) \\ \text{or, } 0 & = (x-1)(x+1)(3x-1) \end{align}
| Either | OR | OR |
|---|---|---|
| \( x - 1 = 0 \) | \( x +1 = 0\) | \( 3x -1 = 0 \) |
| or, \( x = 1 \) | or, \( x = -1 \) | or, \( x = \frac{1}{3} \) |
\( \therefore x= \pm 1, \frac{1}{3} \)
(d) \( x^3-3x^2-9x-5=0 \)
Solution:
Let, \( f(x) = x^3-3x^2-9x-5=0 \)
Possible factors of 5 are \( \pm 1, \pm 5 \)
\begin{align} f(-1) & = (-1)^3-3(-1)^2-9(-1)-5 \\ & = -1-3+9-5 \\ = & 0 \end{align}
\( \therefore x +1 \) is a factor of \( f(x) \)
Now using synthetic division, we get,
\begin{align} \text{Quotient } & = x^2-4x-5 \\ & = x^2 -5x+x-5 \\ & = x(x-5) + 1(x-5) \\ & = (x-5)(x+1) \\ \therefore f(x) & = (x+1)(x+1)(x-5) \\ \text{or, } 0 & = (x+1)(x+1)(x-5) \end{align}
| Either | OR | OR |
|---|---|---|
| \( x + 1 = 0 \) | \( x + 1 = 0\) | \( x - 5 = 0 \) |
| or, \( x = -1 \) | or, \( x = -1 \) | or, \( x = 5 \) |
\( \therefore x = -1, -1, 5 \)
(e) \( x^3 – 3x^2 – 10x + 24 = 0 \)
Solution:
Let, \( f(x) = x^3 – 3x^2 – 10x + 24 \)
Possible factors of 24 are \( \pm 1, \pm 2, \pm 3, \pm 4, \pm 6, \pm 8, \pm 12, \pm 24 \)
\begin{align} \text{Now, } f(2) & = 2^3 -3(2)^2-10(2)+24 \\ & = 8-12-20+24\\ & = 32 - 32 \\ & = 0 \end{align}
\( \therefore x -2 \) is a factor of \( f(x) \)
Now, using synthetic division, we get,
\begin{align} \text{Quotient } & = x^2-x-12 \\ & = x^2 -(4-3)x -12 \\ & = x^2 -4x+3x-12 \\ & = x(x-4)+3(x-4) \\ & = (x-4)(x+3) \\ \therefore f(x) & = (x-2)(x-4)(x+3) \\ \text{or, } 0 & = (x-2)(x-4)(x+3) \end{align}
| Either | OR | OR |
|---|---|---|
| \( x - 2 = 0 \) | \( x - 4 = 0\) | \( x + 3 = 0 \) |
| or, \( x = 2 \) | or, \( x = 4 \) | or, \( x = -3 \) |
\( \therefore x = 2,4,-3 \)
(f) \( y^3 + 11y = 6y^2 + 6 \)
Solution:
Given,
\( y^3+11y=6y^2+6 \\ or, y^3-6y^2+11y-6 = 0 \)
\( \text{Let, } f(y) =y^3-6y^2+11y-6 \)
Possible factors of 6 are \( \pm 1, \pm 2, \pm 3, \pm 6 \)
\begin{align} \text{Now, } f(1) & = 1^3-6(10^2+11(1)-6 \\ & = 1-6+11-6 \\ & = 0 \\ \end{align}
\( \therefore y-1 \) is a factor of \( f(y) \)
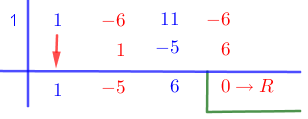
Now, using synthetic division, we get,
\begin{align} \text{Quotient } &= y^2-5y+6 \\ & = y^2 - 3y -2y + 6 \\ & = y(y-3) -2(y-3) \\ & = (y-3)(y-2) \\ \therefore f(y) & = (y-1)(y-2)(y-3) \\ \text{or, } 0 & = (y-1)(y-2)(y-3) \end{align}
| Either | OR | OR |
|---|---|---|
| \( y - 1 = 0 \) | \( y - 2 = 0\) | \( y - 3 = 0 \) |
| or, \( y = 1 \) | or, \( y = 2 \) | or, \( y = 3 \) |
\( \therefore y = 1,2,3 \)
0 Comments